Effects of Harmonic Currents on Power System Part 1

Click on the Registration link above for a Free Account so you can access training and videos as I add them as we go along.

For those interested to get a copy of a Professional Electrical Engineer (Philippines) Technical Engineering Report HERE, login required to access.

Introduction

As an electrical practitioner or electrical engineering student, you probably heard and read many times that Triplen or 3rd Harmonics are bad for your electrical system because they cause higher than normal currents on your neutral wire.

During my review when I was studying for my NCEES Professional Engineer Power Exam, I encountered this topic once again but the review books I’ve read didn’t offer the explanation how exactly these triplen harmonics add up in the neutral conductor.

My curiosity took over and it took me couple days searching Google for an exact sample problem that shows me exactly how and why it is said that instead of cancelling each other like the fundamental currents (60 Hz), these triplen harmonics (180 Hz) add up together. I didn’t found what I was looking for and then finally realized the solution was just in front of me. But I was surprise that a topic this important didn’t get much attention as far as showing sample calculations to prove this concept.

So I decided that in this post, I will offer a clearer, easy to digest explanation about this subject.

Review of Fundamental 3-Phase Electrical Circuits

Below I will try to discuss how the Fundamental (60Hz) Currents cancel each other in the neutral conductor, provided that the load is balanced. Meaning that the currents in all three phases has the same magnitude.

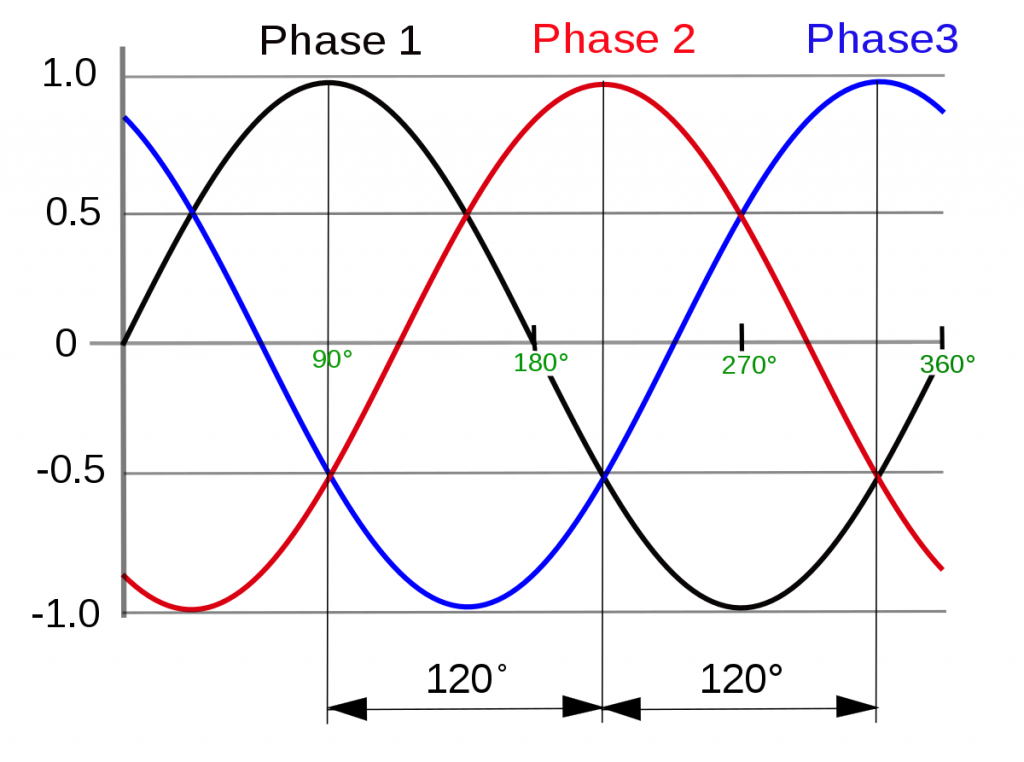
**Figure-1: 3-Phase Alternating Current Waveform**

Figure-1 above is our 3-phase AC waveform fundamental frequency. As you can see, that at every point the total sum of the three currents will equal to zero. For instance, look at angle 90 degrees – the magnitude of Phase 1 is equal to 1 per unit (p.u.), the magnitude of Phase 2 is -0.5p.u. and for the magnitude of Phase 3 is also -0.5p.u. The sum is of course zero.

Try to inspect at all angles from zero to 360 degrees and you will find that the sum of the three phases is always zero.

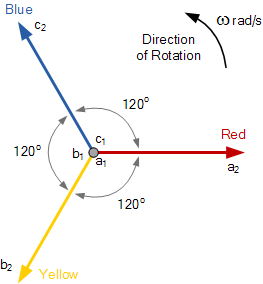
To further illustrate this concept, look at Figure-2 above and then let us write down below the currents in complex form:

Ia = 1 ∠0 p.u., Ib = 1 ∠-120 p.u. , Ic = 1 ∠120 p.u.
In = Ia + Ib + Ic = 0; In = Neutral Current

Now that we have proven using visual inspection and with complex number calculations that balanced 3-phase fundamental currents indeed cancel out each other in the neutral conductor, let’s proceed to investigate triplen harmonics.

How Triplen Harmonics Behave in the Neutral Conductors

First of all, what are triplen harmonics? These are the harmonic currents with frequencies in the multiples of three – such as 3rd (180Hz), 6th(360Hz), 9th(540Hz), 15th(900Hz), etc…

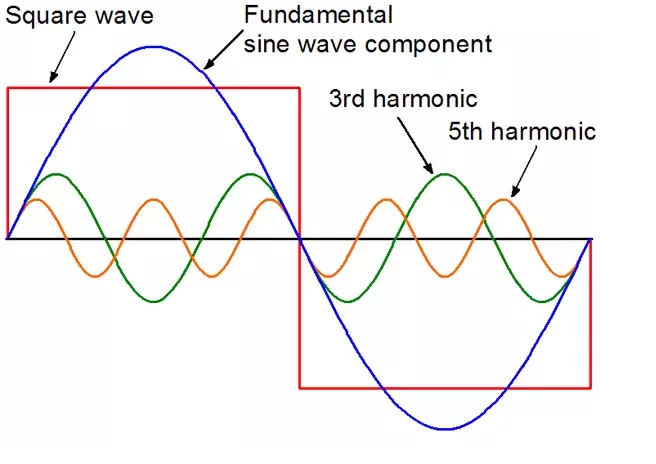
Figure-3 above shows us the fundamental, 3rd and 5th harmonic current sine waves. Looking at the drawing doesn’t immediately tell us how the 3rd harmonic cancel each other . However by evaluating the following formula will give us clearer picture.

$Ei = Em sin(\omega t)$

Where:
Ei = Instantaneous Voltage
Em = Maximum Voltage
$\omega t$ = 2 $\pi ft$

This formula can then be re-written for nth harmonics as follows

$Ei(nth) = En sin(n\omega t)$

Where:
Ei(nth) = Instantaneous Voltage at nth harmonic
En = Maximum Voltage Magnitude at nth harmonic
n $\omega t$ = n2 $\pi ft$ ; example 3 x 2 $\pi ft$ = 6 $\pi ft$

Because this is a three phase circuit, let us consider the phase angle as follows

$Ei = Em sin(\omega t + \phi )$ for fundamental

$Ei(nth) = En sin(n(\omega t + \phi ))$ for general equation

Let us test the formula then

For fundamental frequency:

Phase a Voltage @ time = 0 Sec, Em = 1p.u., Angle = 0 degree

$Ei = Em sin(\omega t + \phi )$
$Ei(Phase a) = 1p.u. sin(3(2\pi60x0 + 0deg ))$
$Ei(Phase a) = 0$

Phase b Voltage @ time = 0 Sec, Em = 1p.u.. Angle = -120 degree

$Ei = Em sin(\omega t + \phi )$
$Ei(Phase b) = 1p.u. sin(2\pi60x0 - 120deg )$
$Ei(Phase b) = -0.866$

Phase c Voltage @ time = 0 Sec, Em = 1p.u.. Angle = 120 degree

$Ei = Em sin(\omega t + \phi )$
$Ei(Phase c) = 1p.u. sin(2\pi60x0 + 120deg )$
$Ei(Phase c) = 0.866$

Now adding Phase a, Phase b and Phase c to get the neutral current. For simplicity, lets assume the impedance load to be 1p.u. as well, therefore

In = Ia + Ib + Ic = 0 + -0.866 + 0.866 = 0

As we can see, the instantaneous formula is consistent with the complex formula and visual inspection we discussed above for the fundamental currents.

Finally let’s apply above concepts to triplen harmonics.

Using complex number calculations, we get the following for a 3rd harmonic.

Ia = 1 ∠0 p.u.
Ib = 1 ∠(3 x -120) p.u.
Ic = 1 ∠(3 x 120) p.u.

In = Ia + Ib + Ic = 1 ∠0 + 1 ∠-360 + 1 ∠360 = 3

As you can see, the 3rd harmonic phase currents did not cancel out each other, instead they have added.
Note that in reality, harmonic current magnitude are less than the fundamental. We just use 1p.u. for ease of calculations.

Now using instantaneous voltage and current formula, let’s see if the same is true. Keeping in mind that we already proven once that 3rd harmonic currents are in-phase with each other which means that their instantaneous values are the same for a specific given time. Which means that all three phase fluctuates (rise and fall) in the plot curve together at the same time.

This means if I pick time = 0 then all three phase will have instantaneous values of zero as shown below.

For 3rd harmonic frequency:

Phase a Voltage @ time = 0 Sec, Em = 1p.u., Angle = 0 degree

$Ei(nth) = En sin(n(\omega t + \phi ))$
$Ei(Phase a) = 1p.u. sin(3(2\pi60x0 + 0deg))$
$Ei(Phase a) = 0$

Phase b Voltage @ time = 0 Sec, Em = 1p.u.. Angle = -120 degree

$Ei = Em sin(\omega t + \phi )$
$Ei(Phase b) = 1p.u. sin(3(2\pi60x0 - 120deg))$
$Ei(Phase b) = 0$

Phase c Voltage @ time = 0 Sec, Em = 1p.u.. Angle = 120 degree

$Ei = Em sin(\omega t + \phi )$
$Ei(Phase c) = 1p.u. sin(3(2\pi60x0 + 120deg))$
$Ei(Phase c) = 0$

As expected, all the three phases have the same value of zero which means they are in-phase with each other and will add up not cancel each other. If instead of using time = 0, we select a time where all of them are at their peak value such as at a time at 90 degree, that time would be

t = 1/720 seconds

Substituting t = 1/720 seconds to the three equations above will result to instantaneous phase current value of 1p.u. for all of the 3 phases and thus the neutral current will become 3p.u. instead of zero.

To be continued on Part 2…

Please share if this has been helpful.

References

National Electrical Code, NFPA 70 2017
IEEE Std 519-1992 Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems
IEEE Std 141-1993 Recommended Practice for Electric Power Distribution for Industrial Plants
Electrical Machines, Drives and Power Systems Sixth Edition by Theodore Wildi